【図解】グラフの平行移動がなぜマイナスで書かれるか本気で解説してみた

こんにちは、そのはです。

先日、グラフの平行移動が式の上ではマイナスで表現されることに納得ができない、という意見をいただきました。私も当時は暗記で済ませていましたが、直感に反していますし深く考えてみると本当にそれでよいのか不安になってきます。

いろいろな解説サイトを見てみても、「$X,Y$を$x,y$と書き直して…」「移動先から逆に考えると…」と誤魔化しつつ説明しているところがほとんどで、高校数学で完結させつつ完璧に納得できるような解説がなされているものは見当たりませんでした。

そこで今回は、グラフの平行移動の式を完璧に納得できるような解説を目指してみます。

平行移動の式のおさらい

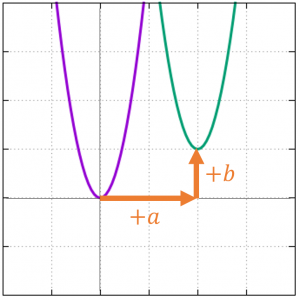
まずは平行移動の式のおさらいです。

$y=f(x)$のグラフを$x$軸方向に$+a$、$y$軸方向に$+b$だけ平行移動するとき、平行移動後のグラフの式は以下のように書けます。

$$y-b=f(x-a)$$

$f(x)$という書き方にピンと来ない場合は具体例を見てみましょう。

$$\begin{align}y&=x&\rightarrow\quad y-b&=x-a\\y&=x^2&\rightarrow\quad y-b&=(x-a)^2\end{align}$$

要は$x$を$x-a$に、$y$を$y-b$に置き換えれば平行移動したことになりますよ、ということです。

この式の問題点

が、なぜマイナスなのでしょう？

よくある説明の仕方は高校数学の美しい物語さんや受験の月さんのように、移動後の座標を$(X,Y)$と置いて$x,y$と$X,Y$の関係式を使って式変型をし、最後に$X,Y$を$x,y$と書き直しておしまい、というものです。
一応それらしい証明ですし、間違っていることは言っていないのですが、最後がいかにも強引で「あれ？$X=x,Y=y$なんだっけ？？」となってしまいます。

これは定数と変数を混同してしまっているために生じるパラドックスです。
この違和感を解消するために、①定数と変数を切り分けた説明と、定数を使わない②変数変換を用いた説明の2通りでグラフの平行移動を説明してみます。

定数と変数を切り分けた説明

平行移動する前のグラフ上のある点を$(p_1,q_1)$とします。この点$x=p_1,y=q_1$は$y=f(x)$を満たすので、$q_1=f(p_1)$が成り立ちます。

また平行移動する前のグラフ上の別の点を$(p_2,q_2)$とします。この点$x=p_2,y=q_2$も$y=f(x)$を満たすので、$q_2=f(p_2)$が成り立ちます。

つづいて平行移動する前のグラフ上のあらゆる点を$(p_i,q_i)$とします。これらすべての点$x=p_i,y=q_i$は$y=f(x)$を満たすので、$q_i=f(p_i)$が成り立ちます。

さて、$(p_1,q_1),(p_2,q_2),…,(p_i,q_i),…$を$x$軸方向に$+a$、$y$軸方向に$+b$だけ平行移動させた点を$(P_1,Q_1),(P_2,Q_2),…,(P_i,Q_i),…$とします。
$i$番目の点には以下のような関係が成り立っています。

$$\begin{align}p_i+a&=P_i\\q_i+b&=Q_i\end{align}$$

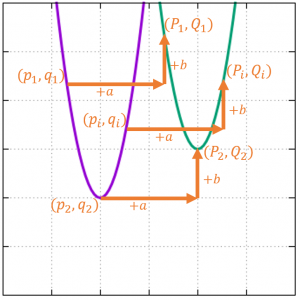
いま知りたいのは$x=P_i,y=Q_i$が満たす関数$y=g(x)$を$f()$で表すとどうなるか、です。

$Q_i=g(P_i)$がどんな式かを$Q_i=q_i+b$を用いて考えると、

$$\begin{align}Q_i=g(P_i)&=q_i+b\\&=f(p_i)+b\\&=f(P_i-a)+b\end{align}$$

と書けます。$g(P_i)=f(P_i-a)+b$はあらゆる点で成り立つので、これを変数$x$で一般化すると$g(x)=f(x-a)+b$となります。

すなわち、平行移動後のグラフの式は

$$y=g(x)=f(x-a)+b\\⇔y-b=f(x-a)$$

です。

定数$p_i,q_i,P_i,Q_i$を用いることで、変数の矛盾なく説明できました。

変数変換を用いた説明

平行移動する前のグラフ上の点を$(x,y)$とし、この$x,y$は$y=f(x)$を満たすとします。

ここで、平行移動した後のグラフ上の点を$(X,Y)$とすると、通常はこの$X,Y$は$Y=f(X)$を満たしません。
これは具体的な値を考えれば分かります。例えば$y=f(x)=x^2$について、このグラフ上にある$(2,4)$は当然$y=f(x)$を満たします。ではこれを$x$軸方向に$+1$、$y$軸方向に$+2$だけ平行移動させた点$(3,6)$は元の関数$y=f(x)$を満たすでしょうか？満たしませんね。
同様に、平行移動後のグラフ上の点$(X,Y)$も$Y=f(X)$を満たしません。

$X,Y$が$Y=f(X)$を満たすような状況を生み出すには、新たな軸を用意する必要があります。

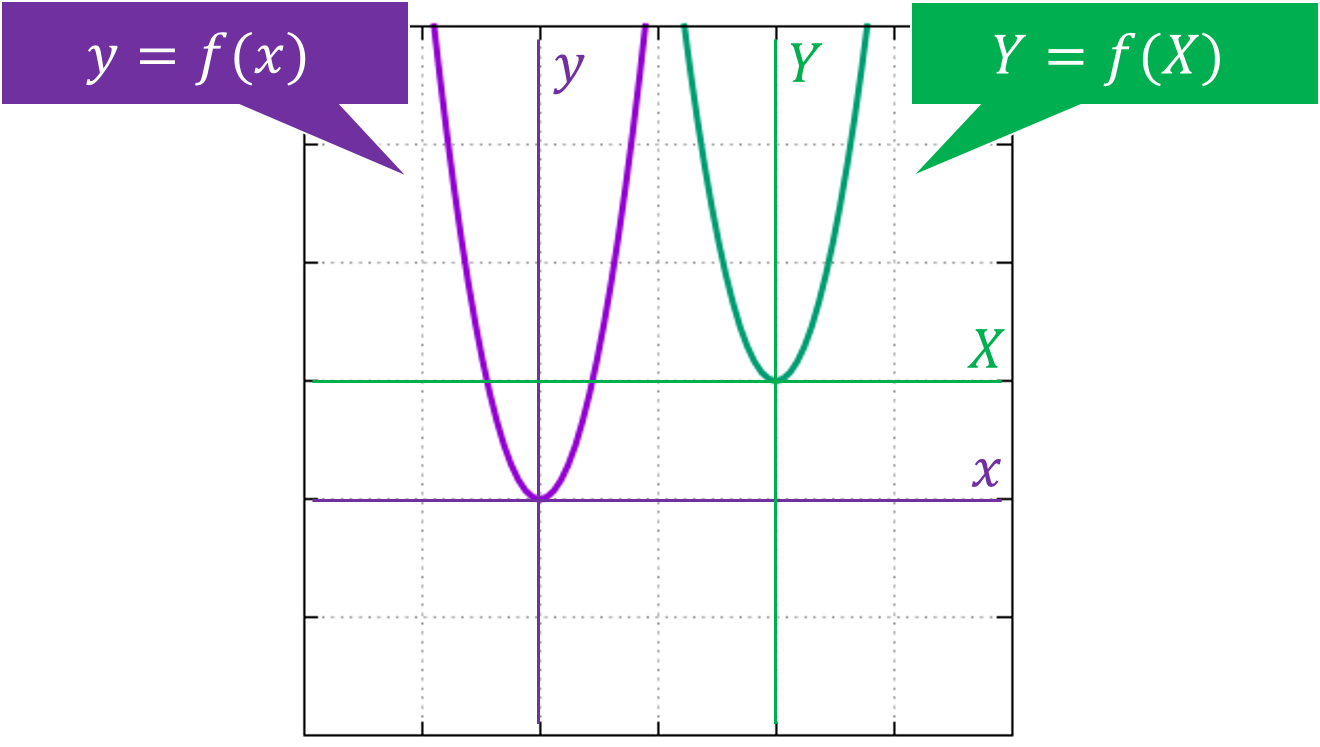
軸ごと平行移動してしまえば、$XY$平面上では$Y=f(X)$が成り立ちます。
このように別の変数を設けて別の軸で考えることを変数変換といいます。

$xy$軸から見た平行移動後のグラフの式が$y=g(x)$と表せるとします。$y=g(x)$も$Y=f(X)$も平行移動後のグラフを表していることに変わりはないので、これらは同値です。

$$y=g(x)⇔Y=f(X)$$

さて、$xy$平面と$XY$平面との位置関係を考えてみましょう。
$xy$軸が$x$軸方向に$+a$、$y$軸方向に$+b$だけ平行移動した結果$XY$軸になったとします。このとき、各平面上の点の対応は、例えば

$$\begin{align}(x,y)=(a,b)&⇔(X,Y)=(0,0)\\(x,y)=(0,0)&⇔(X,Y)=(-a,-b)\end{align}$$

となっています。すなわち$(X,Y)$を$x,y$で表すと、

$$(X,Y)=(x-a,y-b)$$

と書けます。これを$Y=f(X)$に当てはめると、

$$Y=f(X)\\⇔y-b=f(x-a)$$

の関係が導けます。

まとめ

今回は詳しめ且つ少し変わったアプローチで、グラフの平行移動における式がマイナスで書かれることを説明していきました。

慣れるまではどうしても直感と反しているように感じますが、変数と定数を区別して考えたり、軸ごと移動させたりすることで、その相対関係からマイナスで表すことが相応しいことを説明できます。

平行移動は数学において大事な要素のひとつなので、丸暗記ではなく、自分で納得できる形で理解しておきましょう！

それでは。