【解説】3倍角の公式を使って軌跡を導く【東大2017】
この問題の解き方を教えて頂けませんか?🙏
3倍角の公式を使う軌跡の問題ですね!
問題
実数$a,b$に対して、
$$f(\theta)=\cos{3\theta}+a\cos{2\theta}+b\cos{\theta}$$
とし、 $0<\theta<\pi$で定義された関数
$$g(\theta)=\frac{f(\theta)-f(0)}{\cos{\theta}-1}$$
を考える。
(1) $f(\theta)$と$g(\theta)$を$x=\cos{\theta}$の整式で表せ。
(2) $g(\theta)$が$0<\theta<\pi$の範囲で最小値$0$をとるための$a,b$についての条件を求めよ。また、条件を満たす点$(a,b)$が描く図形を座標平面上に図示せよ。
(東京大学 2017年度 理系)
方針
まずやるべきことはn倍角の解消です。
考えやすくするために$\cos{3\theta}$や$\cos{2\theta}$を$\cos{\theta}$に統一します。
(1)は、整理した式をひたすら定義に従って整理していきます。
(2)は、定義域に注意しつつ二次関数の性質を利用して$a$と$b$の関係式を導きます。
解説
$f(\theta),g(\theta)$を$x$で表す
倍角の公式や3倍角の公式を用いて$f(\theta)$を整理します。
倍角の公式
$$\cos{2\theta}=2\cos^2{\theta}-1$$
3倍角の公式
$$\cos{3\theta}=4\cos^3{\theta}-3\cos{\theta}$$
3倍角の公式は暗記していれば時間短縮になりますが、暗記が苦手な場合は加法定理から簡単に導けます。導出に慣れておけば暗記は不要です。
$$\begin{align}
\cos{3\theta}&=\cos{(\theta+2\theta)}\\
&=\cos{\theta}\cos{2\theta}-\sin{\theta}\sin{2\theta}\\
&=\cos{\theta}(2\cos^2{\theta}-1)-\sin{\theta}(2\sin{\theta}\cos{\theta})\\
&=2\cos^3{\theta}-\cos{\theta}-2(1-\cos^2{\theta})\cos{\theta}\\
&=4\cos^3{\theta}-3\cos{\theta}
\end{align}$$
では、これらを用いて$f(\theta)$を整理していきます。
$$\begin{align}
f(\theta)&=\cos{3\theta}+a\cos{2\theta}+b\cos{\theta}\\
&=(4\cos^3{\theta}-3\cos{\theta})+a(2\cos^2{\theta}-1)+b\cos{\theta}\\
&=4\cos^3{\theta}+2a\cos^2{\theta}+(b-3)\cos{\theta}-a
\end{align}$$
これを$x=\cos{\theta}$を用いて書き換えると、
$$f(\theta)=4x^3+2ax^2+(b-3)x-a$$
また、$\theta=0$のとき$x=\cos{0}=1$を用いて、
$$\begin{align}
g(\theta)&=\frac{f(\theta)-f(0)}{\cos{\theta}-1}\\
&=\frac{\{4x^3+2ax^2+(b-3)x-a\}-\{4\cdot1^3+2a\cdot1^2+(b-3)\cdot1-a\}}{x-1}\\
&=\frac{4x^3+2ax^2+(b-3)x-2a-b-1}{x-1}\\
&=4x^2+(2a+4)x+(2a+b+1)
\end{align}$$
(1)答
$$\begin{cases}
f(\theta)=4x^3+2ax^2+(b-3)x-a\\[5pt]
g(\theta)=4x^2+(2a+4)x+(2a+b+1)
\end{cases}$$
$g(\theta)$が最小値$0$をとる$a,b$の条件
ここから先は基本的に$\theta$ではなく$x$で考えていきたいので、$\theta$の関数$g(\theta)$ではなく新たに$x$の関数として
$$h(x)=4x^2+(2a+4)x+(2a+b+1)$$
を定義しておきます。
また、定義域も$x$基準に直すと、$0<\theta<\pi$より$$-1<x<1$$なので、単純に二次関数の問題として扱うことができます。
$h(x)$の最小値が分かりやすいように平方完成を行います。
$$\begin{align}
h(x)&=4x^2+(2a+4)x+(2a+b+1)\\
&=4\left\{x+\left(\frac{a}{4}+\frac{1}{2}\right)\right\}^2-\frac{a^2}{4}+a+b
\end{align}$$
この二次関数の軸は$x=-(\frac{a}{4}+\frac{1}{2})$になります。
また、この二次関数は下に凸の放物線を描くので、定義域$-1<x<1$の中で最小値を持つためには、軸が定義域内に位置する必要があります。
したがって、
$$-1<-\left(\frac{a}{4}+\frac{1}{2}\right)<1\\
\Leftrightarrow-6<a<2$$
そのうえで、最小値が$0$となるときを考えるので、
$$-\frac{a^2}{4}+a+b=0\\
\Leftrightarrow b=\frac{1}{4}(a-2)^2-1$$
(2)答
$-6<a<2$ かつ $b=\frac{1}{4}(a-2)^2-1$
$(a,b)$の軌跡を図示する
さて、あとは上で求まった条件をグラフとして図示します。
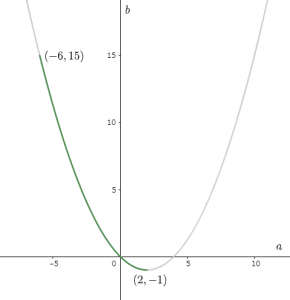
$b$は$a$の二次関数であり、定義域が$-6<a<2$、軸が$x=2$、頂点が$(2,-1)$である下に凸の放物線なので、下の図のとおりになります。
まとめ
東大志望なら必ず取りたい問題ですね!
今回は3倍角の公式を用いて軌跡を求めていくような問題を取り扱いました。
n倍角の部分さえ解消してしまえば、一般的な二次関数の問題に落とし込めるという点では、比較的簡単な問題といえます。ぜひ得点していきたいですね。
仮にn倍角の公式を覚えていなかったとしても、加法定理から瞬時に導けるようにしておくことをおすすめします。
それでは。
-
前の記事

【練習】平均値の定理を使おう 2020.05.04
-
次の記事

1/(xⁿ+1)を積分する【部分分数分解】 2020.07.30














コメントを書く