【図解】グラフの平行移動と座標変換の関係について
積分の変数変換について詳しく考えていたら混乱してきました…。
2種類のアプローチを混同しているようです。
詳しく見ていきましょう。
問題
$$\int_{-\pi-a}^{-\pi+a} f(\cos{x})dx$$
を、積分範囲が$[-a,a]$である積分に直せ。
要するに$f(\cos{x})$を$x$軸方向に$+\pi$だけずらしたいということですね。
こういった問題文があったわけではありませんが、とある問題を解いている途中でこのような操作をしたくなったらしいです。
確かに$x=-\pi$まわりで考えるよりは原点まわりで考えられる方がシンプルになりそうです。
2種類のアプローチ
平行移動
おそらく最初に思いつくのは「平行移動」でしょう。
いま、積分範囲が$[-\pi-a,-\pi+a]$の積分を考えているので、被積分関数$f(\cos{x})$のグラフ全体を$x$軸方向に$+\pi$だけ平行移動してしまえば、積分範囲を$[-a,a]$にすることができます。
式変形は次の通りです。
$x\to x-\pi$と書き換えて、
$$\begin{align}
&\int_{-\pi-a}^{-\pi+a} f(\cos{x})dx\\
&\to\int_{-a}^{a} f(\cos{(x-\pi)})dx=\int_{-a}^{a} f(-\cos{x})dx
\end{align}$$
座標変換
別の方法として、いわゆる「置換」を行うものがあります。
$$\begin{array}{c|ccc}
x&-\pi-a&\to&-\pi+a\\
\hline
t&-a&\to&a\\
\end{array}$$
これを満たすようにするために、$t=x+\pi$と置換します。
式変形は次の通りです。
$x=t-\pi$より$dx=dt$で、
$$\begin{align}
&\int_{-\pi-a}^{-\pi+a} f(\cos{x})dx\\
&=\int_{-a}^{a} f(\cos{(t-\pi)})dt=\int_{-a}^{a} f(-\cos{t})dt
\end{align}$$
$t$は単なる積分変数なので別の文字に書き換えてもよくて、
$$\int_{-a}^{a} f(-\cos{t})dt=\int_{-a}^{a} f(-\cos{x})dx$$
結果は、平行移動でアプローチした場合と一致します。
平行移動と座標変換は同値
「今回のように$dx=dt$であるような場合は」という話ですが。
(厳密には「座標変換⊃平行移動」です。詳しくは線形代数の話になります。)
上の式変形を見ても分かる通り、行う計算も事実上変わりません。
アプローチの違いを図に表してみると次のような感じ。
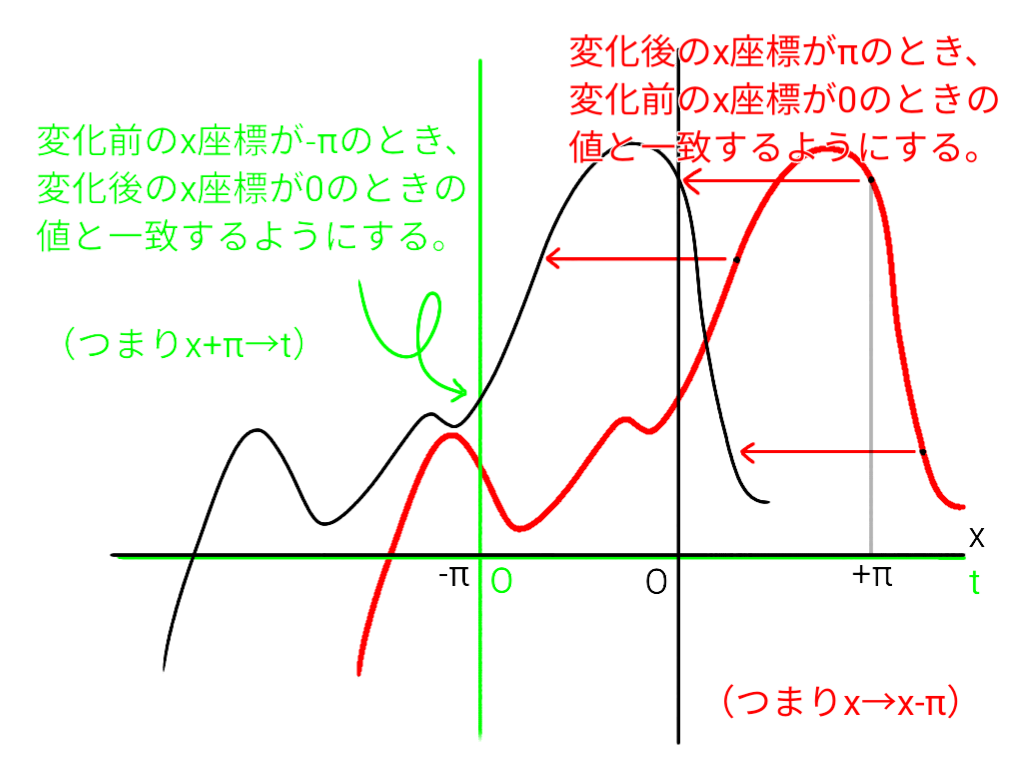
黒いグラフと座標軸がもとの関数、
赤いグラフが平行移動後のグラフ、
緑の軸が座標変換後の軸です。
グラフを動かすのが平行移動、軸を動かすのが座標変換というイメージです。
「黒い軸に対する赤いグラフ」と「緑の軸に対する黒いグラフ」の位置関係は変わらないので、結果は同値です。
まとめ
一見すると別物に感じる平行移動と座標変換ですが、実は似た者同士です。
余計に分かりにくい!という声もあるかもしれませんが、
問題によって平行移動の方がイメージしやすい場合と座標変換の方がイメージしやすい場合とがあると思うので、使い分けていけるといいですね!
それでは。
-
前の記事

【勉強法】数学に「センス」や「直感」はいらない!! 2018.10.30
-
次の記事

【裏技】二直線のなす角、加法定理を使わない求め方【センター2007】 2019.01.02













コメントを書く