【図解】円錐の回転体を図示してみよう【東大2017,阪大2013】

SUMMARY

問題

点$O$を原点とする座標空間内で、一辺の長さが$1$の正三角形$OPQ$を動かす。また、点$A(1,0,0)$に対して、$∠AOP$を$\theta$と置く。ただし$0^\circ≦\theta≦180^\circ$とする。

(1)
点$Q$が$(0,0,1)$にあるとき、点$P$の$x$座標がとりうる値の範囲と、$\theta$がとりうる値の範囲を求めよ。

(2)
点$Q$が平面$x=0$上を動くとき、辺$OP$が通過しうる範囲を$K$とする。$K$の体積を求めよ。

$xyz$空間内の3点$O(0,0,0),A(1,0,0),B(1,1,0)$を頂点とする三角形$OAB$を$x$軸のまわりに1回転してできる円錐を$V$とする。

円錐$V$を$y$軸のまわりに1回転してできる立体の体積を求めよ。

これらの問題は最終的にまったく同じ内容を表しています。
今回はこれを図示することを考えてみます。

詳しい解説はこちらから（外部リンク）。

平面を回転させて立体を作るならばまだイメージしやすいですが、立体を回転させて立体を作るのはかなり想像しにくいです。

円錐に限らず、柱やその他の立体を回転させるのが面倒なんですね…。

阪大の回転体をシミュレートしている図を発見しました。

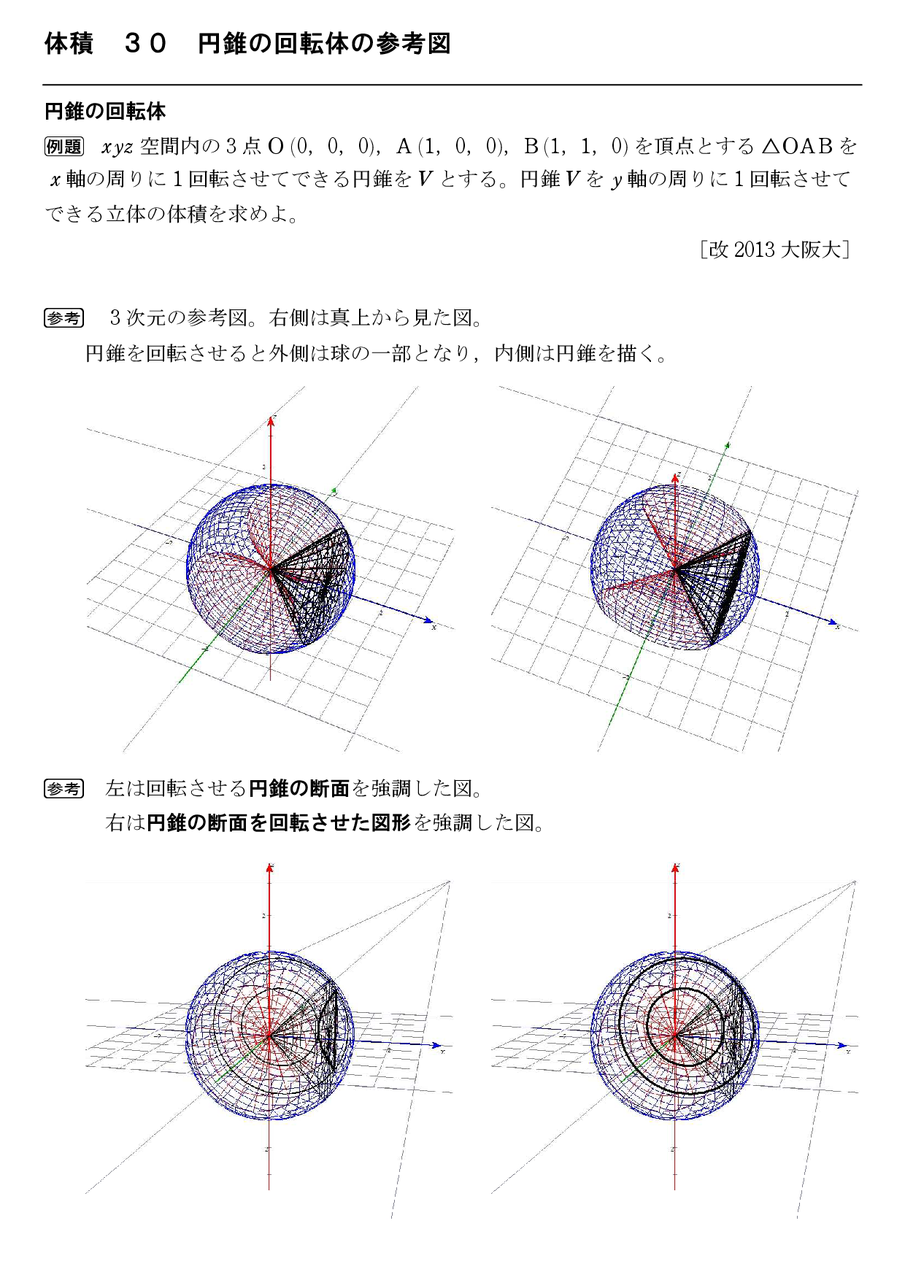黒い円錐が回転させる円錐、
青い立体が出来上がる立体（球から赤い部分をくり抜いた形）。

完成図を理解していないと、この絵を見てもなんのことやらって感じでしょうか…(笑)

どうやら、自分で関数を入れてシミュレーションできるツールがあるそうです☟

こちらを使って円錐を回転してみると…、

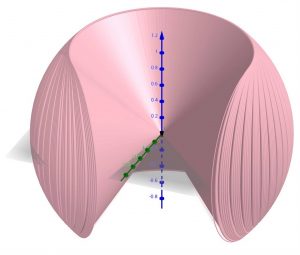
もうちょっと回して…、

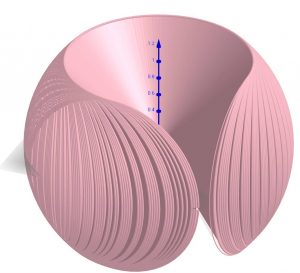
完成した立体を俯瞰すると…、

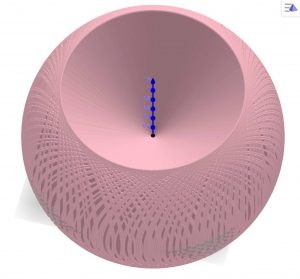
こんな感じです。
さっきよりは分かりやすいかな。

ここでは数式を用いた解説は行いませんが、ポイントとして円錐回転体は円錐底面が球面を描くということです。

円錐に限らず、円を円から離れた軸まわりで回転させると球っぽい領域を描くんですね…。

「回転軸と円錐底面との距離」が場所によって異なるために生じます。

なので、計算の際はその点に注意していきたいですね！

それでは。