【練習】平均値の定理を使おう

問題

解説

問題文にある通り、平均値の定理を使って求めていきます。
ここで、平均値の定理そのものを思い出しておきましょう。

差÷差のような式が出てきたときは、平均値の定理を使わせたい問題である可能性があるので注意していきましょう。

今回の問題では、$f(x)$にあたるのが$e^x$、$a,b$にあたるのが$x,\tan{x}$です。
平均値の定理を使うための前提が成り立っているか確認していきましょう（記述式の場合、この検証は必須です）。

$x,\tan{x}$の大小チェック

この問題で考えたいのは$x\to+0$の極限なので、$x$の範囲としては$0<x<\frac{\pi}{2}$としましょう。
（$x$が正かつ$\tan{x}$が連続である範囲を考えるとこうなります）

$g(x)=x,h(x)=\tan{x}$と置きます。
$g^\prime(x)=1$、$h^\prime(x)=\frac{1}{\cos^2{x}}$より、$0<x<\frac{\pi}{2}$においては$$g^\prime(x)<h^\prime(x)$$です。

さらに、$g(0)=h(0)=0$より、$$g(x)<h(x)\\\Leftrightarrow x<\tan{x}$$となります。

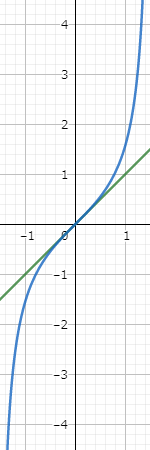
これはグラフを描くと分かりやすいかと思います。
$g(x)=x$も$h(x)=\tan{x}$も$x=0$では同じように原点を通りますが、$x>0$では$h(x)$のほうが傾きが大きいので、$g(x)<h(x)$となります。

$e^x$の連続と微分可能性チェック

$e^x$がすべての範囲で連続かつ微分可能であることは、ことわりなく使ってよいと思います。

なので、ここでの詳しい検証は割愛します。

平均値の定理を使う

以上により、平均値の定理を使う準備が整いました。
では、さっそく使ってみましょう。

与式の分数関数に対して平均値の定理を用いると、$x<c<\tan{x}$を満たすような$c$を用いて、

$$\frac{e^x-e^{\tan{x}}}{x-\tan{x}}=\frac{e^{\tan{x}}-e^x}{\tan{x}-x}=e^c\\
（\because (e^x)^\prime=e^x）$$

と書けます。
なので、いま求めたいのは$$\lim_{x\to+0}e^c$$の値ということになります。

ここで、$x<c<\tan{x}$という条件があるので、はさみうちの原理を使うことができます。

$$\lim_{x\to+0}x=0,\ \lim_{x\to+0}\tan{x}=0\ \Rightarrow\ \lim_{x\to+0}c=0$$

したがって、

$$\lim_{x\to+0}e^c=e^0=1$$

まとめ

今回は平均値の定理の使い方を確認していきました。

平均値の定理はそう頻繁に出てくるものではないですが、少し発展的な問題を解こうとするとしれっと登場することがあります。

以下のポイントに注意して使うことができればOKです。

1回で完璧に理解するのは大変なので、何回か使う中で慣れていきましょう。

それでは。