【練習】三角関数の合成を使ってみよう

$\sin{x}$と$\cos{x}$を両方含む変数の扱いで詰まりました…。

今回は合成が使えそうですね。
一緒に練習していきましょう！

1. 問題
2. 解説
3. まとめ

問題

$0≦\theta≦\pi$のとき、$s=\sqrt{3}\sin{\theta}+\cos{\theta}$、$s=\sqrt{3}\cos{\theta}-\sin{\theta}$とおく。次の問いに答えよ。

(1)　$s^2+t^2$の値を求めよ。

(2)　$s$および$t$のとりうる値の範囲を求めよ。

(3)　$s=-\frac{1}{2}$のとき、$t$の値を求めよ。

解説

先に設問をざっと見てみると、(2)で三角関数の合成を使うことになりそうだと分かります。

なぜかというと、$s$および$t$は$\sin$と$\cos$の2種類の三角関数を含んでおり直接値域を求めることが難しそうであること、そのうえで三角関数の合成が可能である特徴的な式の形をしていること、の2つの特徴があるからです。

特徴的な式の形とは以下のようなものです。

式が$\sin$と$\cos$の和または差で表されている。
その係数が$1,2,\sqrt{3}$など、有名角の三角比に特徴的な値になっている。

後者は必須ではありませんが、合成をいかにも使ってほしそうな問題ではそうなっていることが多いです。

では三角関数の合成公式を振り返ってから、順に問題を解いていきましょう。

三角関数の合成

$$a\sin{\theta}+b\cos{\theta}=
\begin{cases}
\sqrt{a^2+b^2}\sin{(\theta+\alpha)}\\
\sqrt{a^2+b^2}\cos{(\theta-\beta)}
\end{cases}$$

ただし$\alpha,\beta$は、$\tan{\alpha}=\frac{b}{a}$および$\tan{\beta}=\frac{a}{b}$を満たす値。

$s^2+t^2$の値を求める

単純に$s$と$t$の定義を用いて2乗をゴリゴリ計算していくのもよいですが、(2)で合成を使いそうだということが分かっているので、(1)の時点で合成してしまいましょう。
今回は$s$は$\sin$で、$t$は$\cos$で合成してみます（もちろん逆でも両方一緒でもOKです）。

$$\begin{align}
s&=\sqrt{3}\sin{\theta}+\cos{\theta}\\
&=2(\frac{\sqrt{3}}{2}\sin{\theta}+\frac{1}{2}\cos{\theta})\\
&=2(\cos{\frac{\pi}{6}}\sin{\theta}+\sin{\frac{\pi}{6}}\cos{\theta})\\
&=2\sin{(\theta+\frac{\pi}{6})}
\end{align}$$

$$\begin{align}
t&=\sqrt{3}\cos{\theta}-\sin{\theta}\\
&=2(\frac{\sqrt{3}}{2}\cos{\theta}-\frac{1}{2}\sin{\theta})\\
&=2(\cos{\frac{\pi}{6}}\cos{\theta}-\sin{\frac{\pi}{6}}\sin{\theta})\\
&=2\cos{(\theta+\frac{\pi}{6})}
\end{align}$$

したがって、

$$\begin{align}
s^2+t^2&=\{2\sin{(\theta+\frac{\pi}{6})}\}^2+\{2\cos{(\theta+\frac{\pi}{6})}\}^2\\
&=4\{\sin^2{(\theta+\frac{\pi}{6})}+\cos^2{(\theta+\frac{\pi}{6})}\}\\
&=4
\end{align}$$

(1)答

$$s^2+t^2=4$$

$s,t$の値域を求める

合成さえしてしまえば(2)は簡単です。

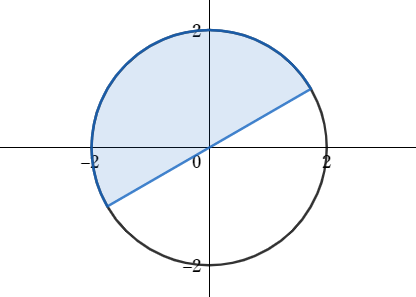
$x=\theta+\frac{\pi}{6}$と置くと、$0≦\theta≦\pi$より$\frac{\pi}{6}≦x≦\frac{7}{6}\pi$。

$\frac{\pi}{6}≦x≦\frac{7}{6}\pi$のとき、$s=2\sin{x}$より、$s$は

$x=\frac{\pi}{2}$すなわち$\theta=\frac{\pi}{3}$のときに最大値$2$
$x=\frac{7}{6}\pi$すなわち$\theta=\pi$のときに最小値$-1$

をとります。

また、$\frac{\pi}{6}≦x≦\frac{7}{6}\pi$のとき、$t=2\cos{x}$より、$t$は

$x=\frac{\pi}{6}$すなわち$\theta=0$のときに最大値$\sqrt{3}$
$x=\pi$すなわち$\theta=\frac{5}{6}\pi$のときに最小値$-2$

をとります。

(2)答

$$-1≦s≦2,\ -2≦t≦\sqrt{3}$$

$s$の値を決めて$t$を求める

(3)は代入するだけです。

$s=-\frac{1}{2}$のとき、$\sin{(\theta+\frac{\pi}{6})}=-\frac{1}{4}$より、

$$\begin{align}
\cos{(\theta+\frac{\pi}{6})}&=\pm\sqrt{1-\sin^2{(\theta+\frac{\pi}{6})}}\\
&=\pm\sqrt{1-\frac{1}{16}}\\
&=\pm\frac{\sqrt{15}}{4}\\
\therefore t&=\pm\frac{\sqrt{15}}{2}
\end{align}$$

(2)より$t$の値域は$-2≦t≦\sqrt{3}$ですが、$\sqrt{3}<\frac{\sqrt{15}}{2}$より$\frac{\sqrt{15}}{2}$は不適。

(3)答

$$t=-\frac{\sqrt{15}}{2}$$